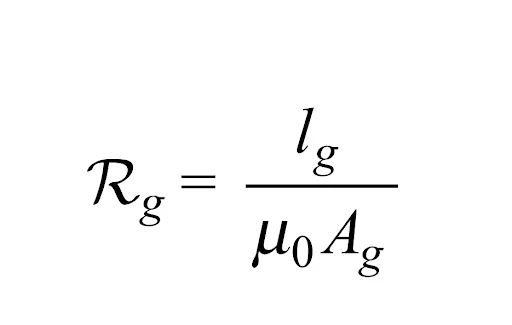MAGNETIC CIRCUIT AND INDUCTION

-
1. Magnetic Circuit Calculations:
Normally magnetic circuit calculations involve two types of problems. In the first type of problem it is
required to determine the excitation (mmf ) needed to establish a desired flux or flux density at a given point
in a magnetic circuit. This is the normal case in designing electromechanical devices and is a straight forward
problem. In the second category, the flux (or flux density) is unknown and is required to be determined for a
given geometry of the magnetic circuit and specified mmf. This kind of problem arises in magnetic amplifiers
wherein this resultant flux is required to be determined owing to the given excitation on one or more control
windings. A little thought will reveal that there is no direct analytical solution to this problem because of the
non-linear B-H characteristic of the magnetic material. Graphical/numerical techniques have to be used in
obtaining the solution of this problem.

2. Leakage Flux:
In all practical magnetic circuits, most of the flux is confined to the intended path by use of magnetic cores but
a small amount of flux always leaks through the surrounding air. This stray flux as already stated is called the
leakage flux, Leakage is characteristic of all magnetic circuits and can never be fully eliminated. Calculations
concerning the main magnetic circuit are usually carried out with the effect of leakage flux either ignored or
empirically accounted for. Special studies of leakage must be made for ac machines and transformers since
their performance is affected by it.


3. Fringing:
At an air-gap in a magnetic core, the flux fringes out into neighbouring air paths as shown
these being of reluctance comparable to that of the gap. The result is nonuniform flux density in the air-
gap (decreasing outward), enlargement of the effective air-
gap area and a decrease in the average gap flux density. The
fringing effect also disturbs the core flux pattern to some
depth near the gap. The effect of fringing increases with the
air-gap length. Corrections for fringing in short gaps (as used
in machines) are empirically made by adding one gap length
to each of the two dimensions making up its area. For the
example of the core with the air-gap previously presented, the
gap reluctance would now be given by
which will be less than the previous value as Ag > A.
It can be shown theoretically that the magnetic flux leaves and enters the surface of an infinitely permeable
material normally. This will be nearly so in ferromagnetic materials which have high permeability. In electric
machines a small amount of the tangential flux component present at iron surfaces will be neglected.

4. Stacking Factor:
Magnetic cores are made up of thin, lightly insulated (coating of varnish) laminations to reduce power loss
in cores due to the eddy-current phenomenon. As a result, the net cross-sectional area of the core occupied by the magnetic material is less than its gross cross-section; their ratio (less than unity) 
being known as the stacking factor. Depending upon the thickness of laminations, stacking factor may vary 
from 0.5–0.95, approaching unity as the lamination thickness increases.

Popular posts from this blog

Short Circuit Test in Transformer

-
Image
Introduction: Transformer me Short Circuit Test ek tarika hai jo hum transformer ke impedance, copper losses, aur dusre parameters ko determine karne ke liye use karte hain. Is test me, transformer ke high-voltage (HV) winding ko short-circuit kar diya jata hai, aur low-voltage (LV) winding pe voltage ko gradually increase kiya jata hai jab tak rated current flow na ho. Translation: The Short Circuit Test in a transformer is a method used to determine the transformer's impedance, copper losses, and other parameters. During this test, the high-voltage (HV) winding is short-circuited, and the voltage on the low-voltage (LV) winding is gradually increased until the rated current flows. Transformer ka Short Circuit Test: Ek Step-by-Step Guide Step 1: Preparation ● Ensure karen ki transformer de-energized aur safely isolated ho. ● Test aksar low-voltage (LV) side pe kiya jata hai, jabki high-voltage (HV) side short-circuited hoti hai. Step 2: Connections ● LV winding ko ek v...
Read more

Magnetism kya hai and It's Application

-
Image
Magnetism ek physical phenomenon hai jo moving charges ya magnets ke interaction ki wajah se hota hai. 1. Magnetism ki Basic Definition Magnetism ek attractive ya repulsive force hai jo magnets aur magnetic materials (iron, cobalt, nickel) ke beech hoti hai. Magnetic force moving electric charges aur magnetic dipoles ke interaction ki wajah se hoti hai. 2. Magnetic Poles Poles: Har magnet ke do poles hote hain North Pole (N) aur South Pole (S). Rule: Like poles repel (N-N, S-S) aur unlike poles attract (N-S). Magnetic poles kabhi alag nahi hote; agar ek magnet ko tod diya jaye, har part ke paas fir bhi ek North aur South pole hoga. 3. Magnetic Field Magnet ke aas-pass ek invisible area hota hai jisme magnetic force kaam karti hai, ise magnetic field kehte hain. Symbol: Magnetic field ko B se denote kiya jata hai. Unit: Magnetic field ki SI unit Tesla (T) hai. Field Lines: Magnetic field lines North se South pole ki taraf jaati hain aur lines dense hone ka matlab stronger field hai....
Read more

Transformer me ferromagnetic material kyu use karte hai?

-
Image
Transformer mein ferromagnetic materials ka use kyun kiya jata hai? Ferromagnetic materials ka use transformer mein mainly unke high magnetic permeability ki wajah se kiya jata hai. High magnetic permeability ka matlab hai ki ye materials magnetic flux ko apne andar se easily pass hone dete hain. Isse kya fayda hota hai?   Zyada magnetic flux: High permeability ki wajah se, transformer mein zyada magnetic flux hota hai, jisse transformer ki efficiency badhti hai. Less core loss: Isse transformer ke core mein kam heat loss hota hai, jisse transformer ki efficiency aur life badhti hai. Small core size: Zyada magnetic flux ko handle karne ke liye, core ko bada nahi banana padta, jisse transformer ka size aur weight kam ho jata hai. Iske alawa, ferromagnetic materials ki aur bhi kuch properties hoti hain jo unhe transformer ke liye suitable banati hain. High saturation point: Ye materials high magnetic field mein bhi apni magnetic properties ko retain rakhte hain, jisse tra...
Read more